Задача 57286 ...
Условие
1) y = √((x - 2) / ((x - 4)(7 - 2x)));
2) y = √x / (2x² - 8);
3) y = 1 / √(9 - x²).
2. Какие преобразования нужно применить к графику функции y = x, чтобы получить график функции y = 4x - 2?
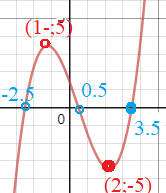
3. Используя данные f(-2,5)=0, f(0,5)=0, f(3,5)=0, xmax =-1, xmin=2 и f(-1)=5, f(2)=-5, постройте схематически график функции y = f(x). По графику найдите промежутки знакопостоянства, возрастания и убывания функции.
Решение
a)
[m]\frac{x-2}{x-4)(7-2x)} ≥ 0[/m] ⇒ [m]\frac{x-2}{(x-4)(2x-7)} ≤ 0[/m]
решаем методом интервалов:
___ [red]-_[/red] _ [2] ___+___ (3,5) __ [red]-[/red] ___ (4) ____+___
[b]О т в е т. (- ∞ ;2]U (3,5;4)[/b]
б)
{x ≥ 0
{2x^2-8 ≠ 0 ⇒ x ≠ ± 2
[b]О т в е т. (0;2) U(2;+ ∞)[/b]
в) 9-x^2 >0 ⇒ (3-x)(3+x) >0
_____ (-3) ___[red]+[/red]___ (3) ______
[b]О т в е т. (-3;3) [/b]
2.
y=x
y=4x - растяжение по оси Оу в 4 раза
y=4x-2 - параллельный перенос ( сдвиг) вдоль оси Оу на 2 единицы вниз
3.