Задача 57057 ...

6003ec49960c3c35933df5fa

17.01.2021 10:57:55

648. Найдите объем прямоугольного параллелепипеда, основания которого равны a и b, а высота равна h, если:
a) a = 11, b = 12, h = 15;
б) a = 5, b = 3√3, h = 13;
в) a = 18, b = 12, h = 10√10;
г) a = 3√2, b = √5, h = 0,96.

649. Найдите объем куба ABCDA₁B₁C₁D₁, если:
a) AC = 12 см;
б) AC₁ = 3√2 м;
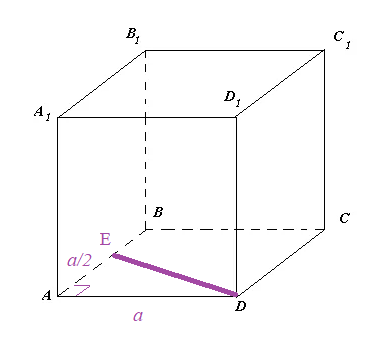
в) DE = 1 см, где Е - середина ребра АВ.

5f3ea7e3faf909182968ddd9

17.01.2021 11:40:45

★

648.
V=S_(осн)*h=a*b*h

a)
V=11*12*15= считайте...

б)
V=3sqrt(2)*sqrt(5)*10sqrt(10)=300

в)
V=18*5sqrt(3)*13=1170sqrt(3)

г)
V=(3 (1/3))*sqrt(5)*0,96=(10/3)*(96/100)*sqrt(5)=3,2sqrt(5)


649
V_(куба)=a^3,
а- сторона куба

a)
AC_(1)- диагональ квадрата АВСD

AC^2=AB^2+BC^2=a^2+a^2=2a^2

AC=12
12^2=2a^2 ⇒ a^2=6; a=sqrt(6)

V=a^3=a^2*a=[b]6*sqrt(6)[/b]

б)
AC_(1)- диагональ куба

AC_(1)=d
d^2=a^2+a^2+a^2
d^2=3a^2

AC_(1)=3sqrt(2)

(3sqrt(2))^2=3a^2 ⇒ 18=3a^2 ⇒ a^2=6
a=sqrt(6)

V=a^3=a^2*a=[b]6*sqrt(6)[/b]

в)
DE^2=DA^2+AE^2 ( cм рис.)

1=a^2+(a/2)^2

1=5a^2/4

a^2=4/5


a=2/sqrt(5)

V=a^3=a^2*a=(4/5)*(2/sqrt(5))=8/(5sqrt(5)=[b]8sqrt(5)/25[/b]