Задача 56935 ...
Условие
lim (z→0) [(2x + 2z) / (x + z + 3) - (2x) / (x + 3)] ÷ z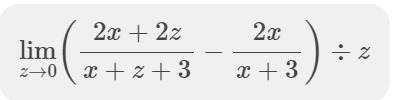
математика ВУЗ
210
Решение
★
[m]lim_{z → 0}(\frac{2x+2z}{x+z+3}-\frac{2x}{x+3}):z=lim_{z → 0}\frac{6z}{z(x+z+3)(x+3)}=\frac{6}{(x+3)^2}[/m]