Задача 56875 Пределы. Помогите решить ...
Условие
математика
186
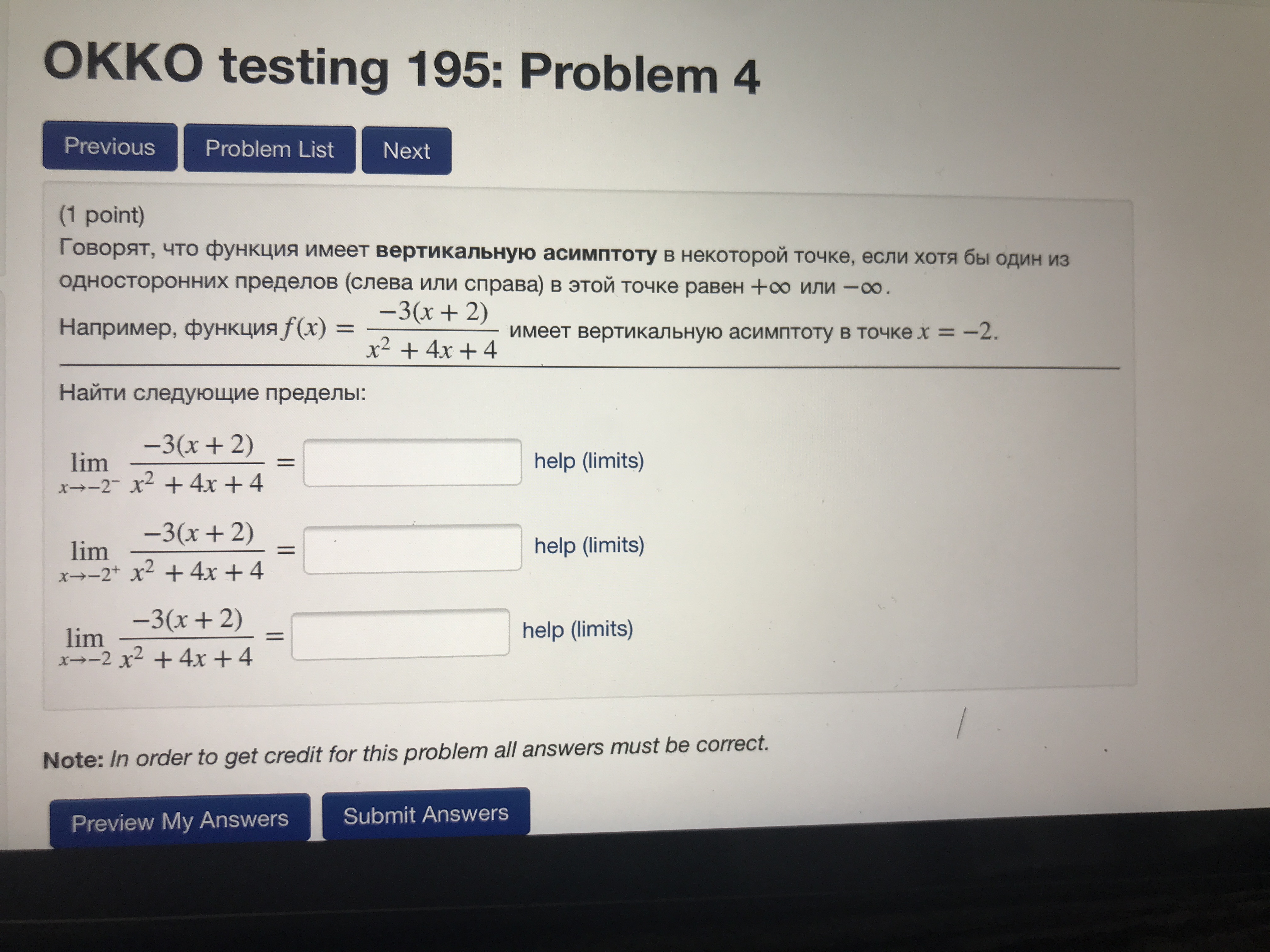
Решение
★
[m]lim_{x →- 2^{-}}\frac{-3(x+2)}{x^2+4x+4}=lim_{x →- 2^{-}}\frac{-3(x+2)}{x+2)^2}[/m]
сокращаем на [m](x+2)[/m]
x → 2 ( но x ≠ -2)
([m]x →- 2^{-}[/m], значит x<-2 и ⇒ x+2 <0) ,
а (-3 делим на очень маленькое отрицательное получаем большое положительное)
[m]=lim_{x →- 2^{-}}\frac{-3}{x+2}=+ ∞ [/m]
2)
[m]lim_{x →- 2^{+}}\frac{-3(x+2)}{x^2+4x+4}=lim_{x →- 2^{+}}\frac{-3(x+2)}{(x+2)^2}[/m]
сокращаем на [m](x+2)[/m]
([m]x →- 2^{+}[/m], значит x>-2 и ⇒ x+2 >0) ,
а (-3 делим на очень маленькое положительное получаем большое отрицательное)
[m]=lim_{x →- 2^{-}}\frac{-3}{x+2}=- ∞ [/m]
3)
[m]lim_{x →- 2}\frac{-3(x+2)}{x^2+4x+4}=∞ [/m]