Задача 56384 ...

5fe1d16c1c6d1142ab515db1

22.12.2020 14:38:10

Задача 2. Сделать чертеж области, ограниченной заданными линиями.

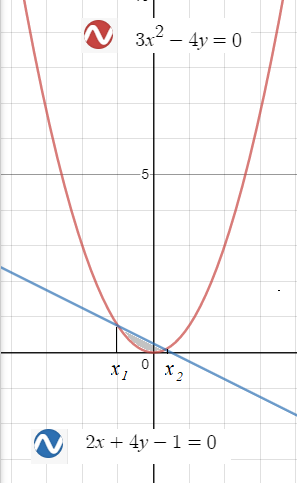
Вычислить площадь полученной фигуры

3х² - 4у = 0; 2х + 4у - 1 = 0.

5f3ea7e3faf909182968ddd9

22.12.2020 14:49:01

★

Сначала найти абсциссы точек пересечения графиков. Решить систему уравнений:
{3x^2-4y=0
{2x+4y-1=0 ⇒ 4y=1-2x

3x^2-(1-2x)=0

3x^2+2x-1=0
x_(1)=-1; x_(2)=1/3

2x+4y-1=0 ⇒ 4y=1-2x ⇒ y=(1-2x)/4
3x^2-4y=0 ⇒ y=(3/4)x^2

[m] S= ∫ ^{\frac{1}{3}}_{-1}(\frac{1-4x}{2}-\frac{3}{4}x^2)dx=[/m]