Задача 56307 ...
Условие
5.27. lim (2x - 13) / (x⁷ - 3x⁵ - 4x).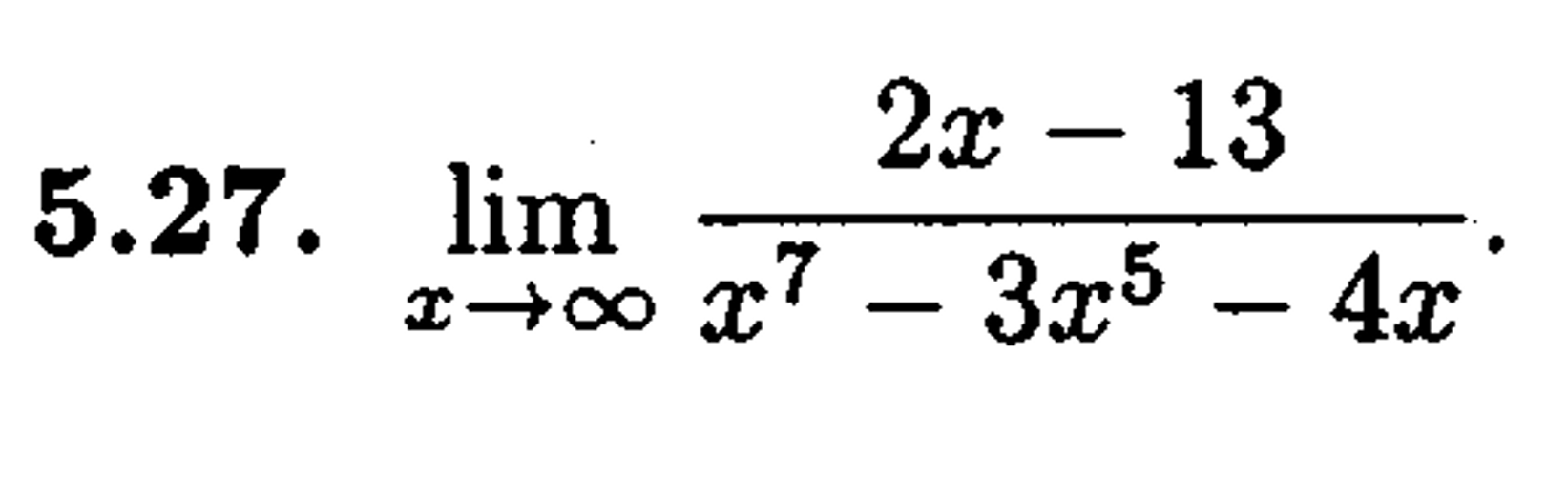
математика ВУЗ
319
Решение
★
Неопределенность ( ∞ / ∞ )
Делим числитель и знаменатель на x^7:
[m]=\lim_{ \to \infty }\frac{\frac{2x-13}{x^7}}{\frac{x^7-3x^5-4x}{x^7}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x^7 и
каждое слагаемое знаменателя делим на x^7:
[m]\lim_{ \to \infty }\frac{\frac{2x}{x^7}-\frac{13}{x^7}}{\frac{x^7}{x^7}-\frac{3x^5}{x^7}-\frac{4x}{x^7}}=[/m]
[m]=\lim_{ \to \infty }\frac{{2}{x^6}-\frac{13}{x^7}}{1-\frac{3}{x^2}-\frac{4}{x^6}}=\frac{0-0}{1-0-0}=0[/m]