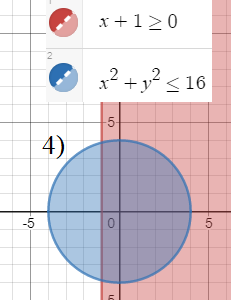Задача 54216 ...
Условие
1)Является ли решением системы неравенств пара значений переменных x и y {x^2 + y^2 ≥ {9 y ≥ x^2 - 3 { -- общая скобка 1)(1; 2); 2)(2; 9); 3)(-3; 0); 4)(-2; -2)
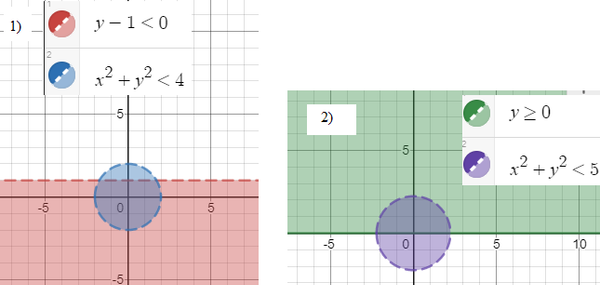
2)На координатной плоскости покажите штриховкой множество точек, координаты которых удовлетворяют системе неравенств: 1) {y - 1 < 0 {x^2 + y^2 <4
4){x + 1 ≥ 0 {x^2 + y^2 ≥ 9 { -- общая скобка
Решение
1)
(1;2)
Подставляем координаты точки в каждое неравенство системы:
[m]\left\{\begin{matrix}
1^2+2^2\geq 9\\2\geq 1^2-3 \end{matrix}\right.[/m][m]\left\{\begin{matrix}
9\geq 9\\2\geq -2 \end{matrix}\right.[/m]
Оба неравенства верные.
О т в е т. является
2)(2;9)
Подставляем координаты точки в каждое неравенство системы:
[m]\left\{\begin{matrix}
2^2+9^2\geq 9\\9\geq 2^2-3 \end{matrix}\right.[/m][m]\left\{\begin{matrix}
85\geq 9\\9\geq 1 \end{matrix}\right.[/m]
Оба неравенства верные.
О т в е т. является
и так далее
6.9