Задача 54170 пожалуйста....
Условие
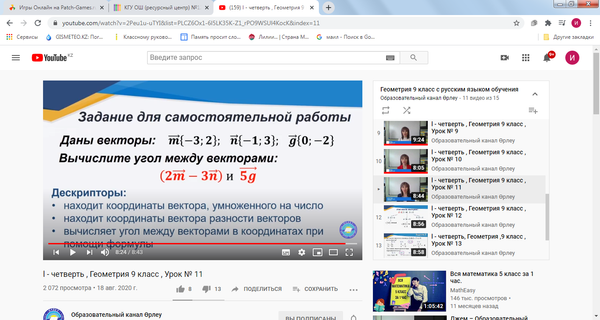
248
Решение
★
[m]5\vec{g}=(5\cdot 0;5\cdot(-2))=(0;-10)[/m]
Скалярное произведение векторов, заданных координатами:
[m]\vec{a}=(x_{a}; y_{a})[/m] и [m]\vec{b}=(x_{b}; y_{b})[/m]
равно сумме произведений одноименных координат ( первую координату [m]\vec{a} [/m] умножаем на первую координату [m]\vec{b}[/m], вторую координату [m]\vec{a}[/m] умножаем на вторую координату [m]\vec{b} [/m] и складываем):
[m]\vec{a}\vec{b}=x_{a}\cdot x_{b}+y_{a}\cdot y_{b}[/m]
Тогда
[m](2\vec{m}-3\vec{n})\cdot 5\vec{g}=(-3)\cdot 0 +(-5)\cdot(-10)=50[/m]