Задача 53460 ...
Условие
1) y = 3 - |x + 5|;
2) y = 4 - |x - 2|;
3) y = 3 - √x - 2;
4) y = 1 - √x + 1 .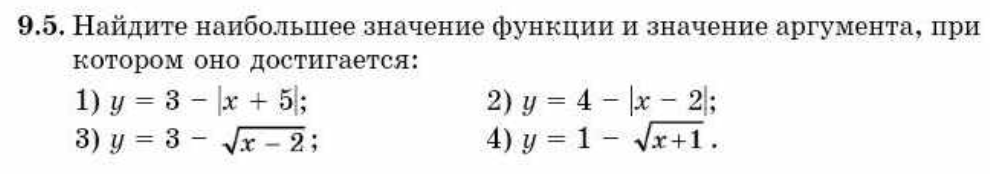
Решение
|x+5|≥ 0
y=|x+5| достигает наименьшего значения [b]0[/b] при x=-5
y=-|x+5| достигает[b] наибольшего [/b]значения 0 при x=-5
y=3-|x+5| достигает[b] наибольшего [/b]значения [b]3[/b] при x=-5
2) аналогично |x-2| ≥ 0
y=|x-2| достигает наименьшего значения 0 при x=2
y=-|x-2| достигает[b] наибольшего [/b]значения 0 при x=2
y=4-|x-2| достигает[b] наибольшего [/b]значения [b]4[/b] при x=2
3)
sqrt(x-2) ≥ 0 при x ≥ 2
y=sqrt(x-2) достигает наименьшего значения [b]0[/b] при x=2
y=-sqrt(x-2) достигает[b] наибольшего [/b]значения 0 при x=2
y=3-sqrt(x-2) достигает[b] наибольшего [/b]значения [b]3[/b] при x=2
4)
sqrt(x+1) ≥ 0 при x ≥ -1
y=sqrt(x+1) достигает наименьшего значения [b]0[/b] при x=-1
y=-sqrt(x+1) достигает[b] наибольшего [/b]значения 0 при x=-1
y=1-sqrt(x+1) достигает[b] наибольшего [/b]значения [b]1[/b] при x=-1