Задача 53264 ...
Условие
∑ (2·5·8⋯(3n-1) / 3·7·11⋯(4n-1)) . (Ответ: сходится.)
n=1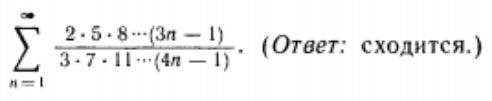
математика ВУЗ
249
Решение
★
[m] lim_{n\rightarrow \infty} \frac{a_{n+1}}{a_{n}}=lim_{n\rightarrow \infty} \frac{\frac{2\cdot 5\cdot 8\cdot ...\cdot (3n-1)\cdot (3n+2)}{3\cdot 7\cdot 11\cdot ...\cdot (4n-1)\cdot (4n+3)}}{\frac{2\cdot 5\cdot 8\cdot ...\cdot (3n-1)}{3\cdot 7\cdot 11\cdot ...\cdot (4n-1)}}=lim_{n\rightarrow \infty}\frac{3n+2}{4n+3}=\frac{3}{4}<1[/m]