Задача 53257 Докажите, что являются нечетными функции...
Условие
7.16. 1) y = -x|x| + x^3;
2) y = -x|x^3|;
3) y = x/(x^2 + 4) - x;
4) y = sqrt(x + 8) - sqrt(8 - x).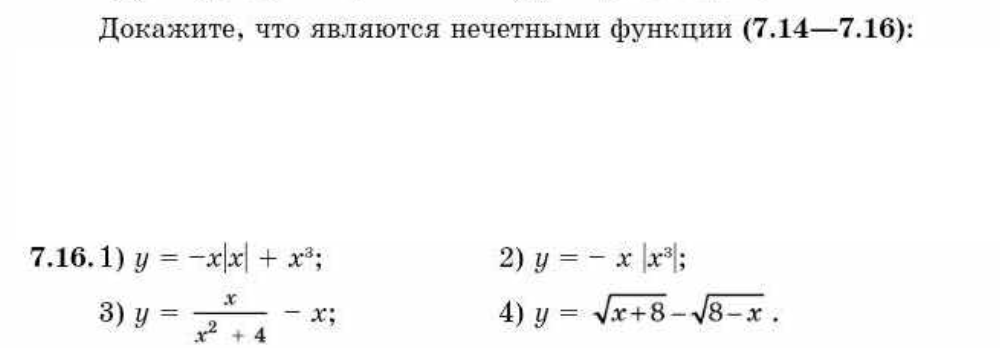
Решение

Все решения
область определения (- ∞ ;+ ∞ ) симметрична относительно 0
и
f(-x)=f(x)
7.16
1)
область определения (- ∞ ;+ ∞ ) симметрична относительно 0
f(-x)=-x|(-x)^3|=-x|-x^3|=-x|x^3|=f(x)
2)
область определения (- ∞ ;+ ∞ ) симметрична относительно 0
f(-x)=-x|(-x)^3|=-x|-x^3|=-x|x^3|=f(x)
3)
область определения (- ∞ ;+ ∞ ) симметрична относительно 0
f(-x)=[m]\frac{-x}{(-x)^2+4}-(-x)=\frac{-x}{x^2+4}+x=-(\frac{x}{x^2+4}-x)
f(-x) ≠ f(x)
4)
область определения (- ∞ ;+ ∞ ) симметрична относительно 0
f(-x)=sqrt(-x+8)-sqrt(8-(-x))=sqrt(8-x)-sqrt(x+8)
f(-x) ≠ f(x)
О т в е т. 1) и 2)