Задача 47113 MABC — правильная треугольная пирамида,...
Условие
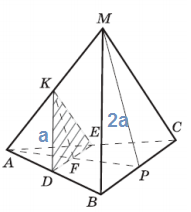
1. Постройте сечение пирамиды плоскостью, проходящей через середины рёбер AB и AC параллельно грани MBC.
2. Вычислите периметр сечения.
3. Вычислите высоту KF сечения.
4. Укажите различные способы вычисления площади сечения.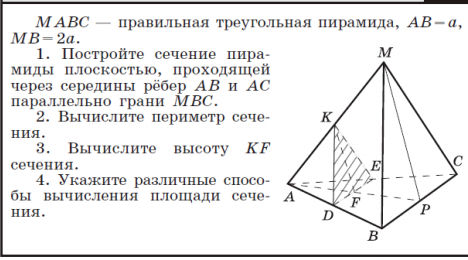
математика 10-11 класс
987
Решение
★
KD=MB/2=a
Аналогично,
КЕ=а
DE-средняя линия Δ АВC
DE=BC/2=[b]a/2[/b]
P=a+a+(a/2)=[b]5a/2[/b]
Δ KDF - равнобедренный
DF=FE=DF/2=a/4
KF^2=KD^2-DF^2=a^2-([b]a/4[/b])^2=15a^2/4
KF=a*sqrt(15)/2
S_( Δ DKE)=(1/2)DE*KF=(1/2)(a/2)*(asqrt(15)/2)=(a^2sqrt(15))/8