Задача 44327 ...
Условие
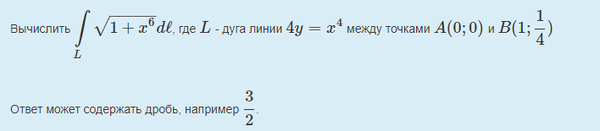
математика
622
Все решения
dl=sqrt(1+(x^3)^2)dx
= ∫ ^(1)_(0)(1+x^6)dx=(x+(x^7/7))|^(1)_(0)=1+(1/7)=8/7
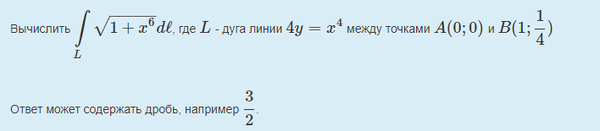
dl=sqrt(1+(x^3)^2)dx
= ∫ ^(1)_(0)(1+x^6)dx=(x+(x^7/7))|^(1)_(0)=1+(1/7)=8/7