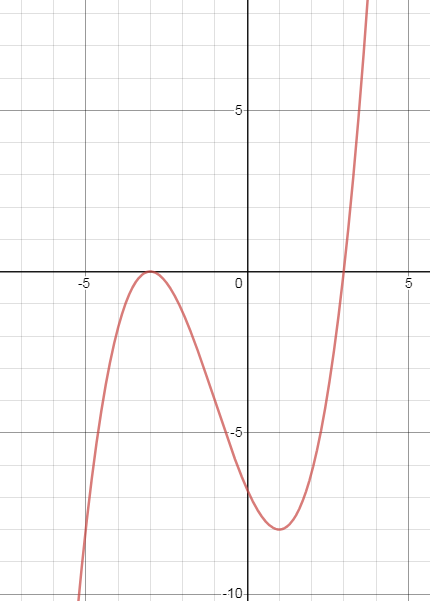
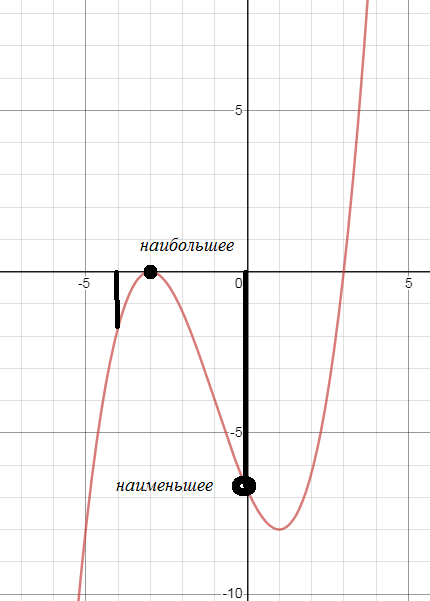
Задача 44153 Исследуйте функцию f(x) = (1/4) (x -...

cmaruh

2020-02-12 12:35:21

Исследуйте функцию f(x) = (1/4) (x - 3)(x + 3)^2 и построите ее график. Найдите наибольшее и наименьшее значение этой функции на отрезке [-4; 0]

sova

2020-02-12 15:11:51

★

Находим производную ( правило : производная произведения)

y`=(1/4)*(x-3)`*(x+3)^2+(1/4)*(x-3)*((x+3)^2))`

y`=(1/4)*(x+3)*(x+3)+2)

y`=(1/4)*(x+3)*(x+5)


y`=0

x=-5 или x=-3

Знаки производной:

__+_ (-5) __-__ (-3) __+__

y`>0 функция возрастает
y`<0 функция убывает