Задача 43918 ...

vk381353806

2020-02-03 19:08:25

8(4). Используя монотонность функций, решите уравнения:
a)(2) 20^x + 21^x = 29^x;
б)(2) 5^(-x) = log_5 (x + 6) + 4.

9(4). Используя монотонность функций, решите неравенства:
a)(2) ⁵√(x − 5) + √(x − 2) < 9 − x^3 / 36;
б(2) 5^(2x − 5) + log_5 (2x − 3) ≥ 5^(4 − x) + log_5 (6 − x).

sova

2020-02-03 21:45:00

★

8
а) Решаем графически:
y=20^(x)+21^(x) - возрастающая на (- ∞ ;+ ∞ ) функция., как сумма возрастающих y=20^(x) и y=21^(x)
(график красного цвета)

y=29^(x) - возрастающая на (- ∞ ;+ ∞ ) функция
(график синего цвета)

При x=0
20^(0)+21^(0)=2

29^(0)=1

2>1

График красного цвета выше графика синего цвета

Кривые не пересекаются.

Уравнение не имеет корней.

б)
Решаем графически:

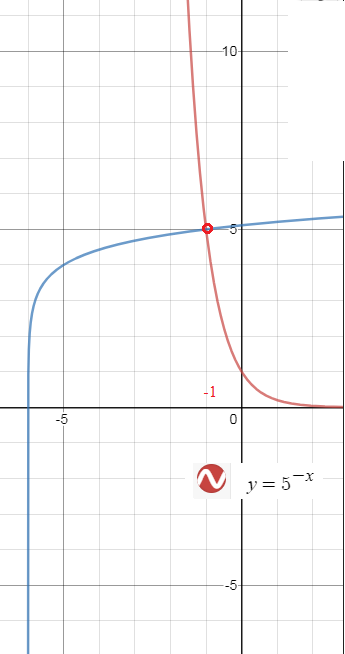
y=5^(-x) - убывающая на (- ∞ ;+ ∞ ) функция


y=log_(5)(x+6)+4 - возрастающая на (-6 ;+ ∞ ) функция


Одна точка пересечения.

Подбором ее находим: x=-1

5^(-(-1))=log_(5)(-1+6)+4

5=5 - верно

Других корней нет

О т в е т. x=-1