Задача 41394 Вариант II 1. Точка K лежит на стороне...

golarina

2019-11-10 18:19:14

Вариант II

1. Точка K лежит на стороне AB, а точка M — на стороне CD параллелограмма ABCD, причем AK=KB, CM:MD=2:5.
a) Выразите вектор KM через векторы p=AB и q=AD. б) Может ли при каком-нибудь значении x выполняться равенство KM=xCB?

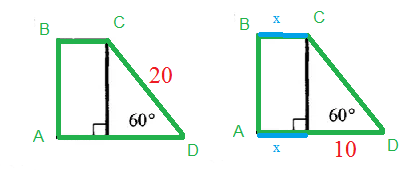
2. Один из углов прямоугольной трапеции равен 120°, большая боковая сторона равна 20 см, а средняя линия равна 7 см. Найдите основания трапеции.

sova

2019-11-10 23:03:08

1.
vector{KM}=vector{KB}+vector{BM}

[b]vector{KM}=(1/2)vector{p}+(5/7)vector{q}[/b]

б) нет, векторы vector{KM} и vector{СB} не коллинеарны.

2.
Сумма углов, прилежащих к боковой стороне трапеции равна 180 градусов.

Пусть угол ∠ C=120 ° , тогда ∠ D=60 °

Проведем высоту из вершины С на сторону AD.
Трапеция разбивается на прямоугольник и прямоугольный треугольник с гипотенузой СD и с острым углом ∠ D=60 ° ,
второй острый угол 30 °

Катет против угла в 30 ° равен половине гипотенузы СВ

Обозначим основание ВС=х

Тогда AD=x+10

(AD+BC)/2=7

AD+BC=2*7

x+10+x=14

x=2

[b]BC=2[/b]
[b]AD[/b]=2+10=[b]12[/b]