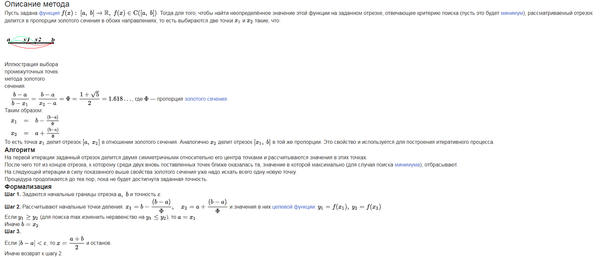
Задача 36094 ...

89283816788

2019-04-19 23:30:00

Задание №3

Используя метод Фибоначчи при заданном значении ε* = 0.1 наибольшей допустимой длины интервала неопределенности найти интервалы, в котором расположима точка х* минимума унимодальной на отрезке [0,1] функции:

1) f(x) = 100(x - 0.2)^2

sova

2019-04-20 14:42:35

x_(1)=1-(2/(1+sqrt(5)))=1+sqrt(5)-2)/(1+sqrt(5))=(sqrt(5)-1)/(sqrt(5)+1)

f(x_(1))=100*((sqrt(5)-1)/(sqrt(5)+1) - 1/5)^2=...

x_(2)=0+ (1/(1+sqrt(5)))=1-sqrt(5)/(1-5)=sqrt(5)-1)/4

f(x_(2))=