Задача 31536 Пусть [m] f(x) = x^2 - 3x + 1, g(x) = |x...

fro99e

2018-12-03 23:37:15

Пусть [m] f(x) = x^2 - 3x + 1, g(x) = |x - 2| [/m].

1. Найдите функции [m] h_1 = f \circ g [/m] и [m] h_2 = g \circ f [/m] и постройте графики этих функций.

sova

2018-12-04 14:59:24

★

1.
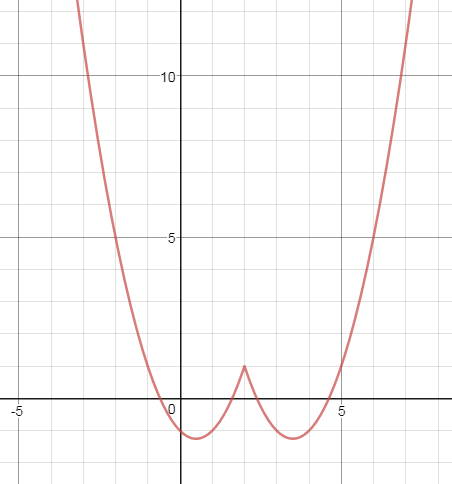
h_(1)(x) = (f o g)(x) = f(g(x))=|x-2|^2-3|x-2|+1
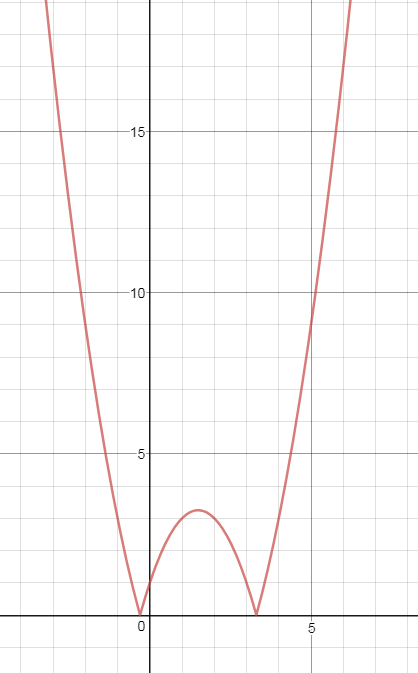
h_(2)(x) = (g o f)(x) = g(f(x))=|x^2-3x+1-2|=|x^2-3x-1|

График функции y=h_(1)(x) на рис. 1

График функции y=h_(2)(x) на рис. 2

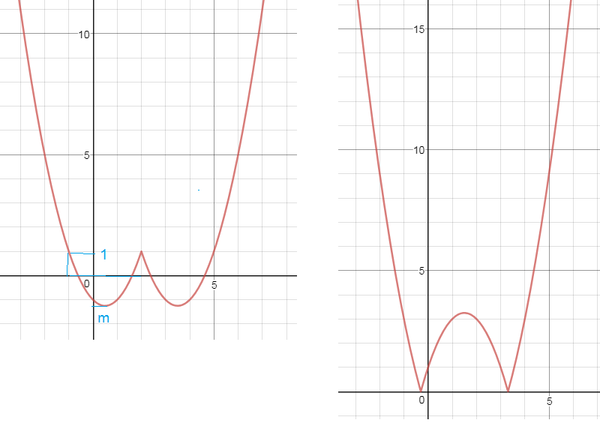
По графику легко найти промежутки монотонности

h_(1) : [-1;2] →[m;1] cм. рис. 3
m- ордината вершины параболы