Задача 28366 ...
Условие
1. Указать предел интегрирования в равенствах для повторных интегралов в декартовой системе координат
2. Найти площадь фигур, ограниченных данными кривыми, с помощью двойного интеграла: y = sin x, y = 0, x = 0, x = π.
3. Вычислить объем области, ограниченной заданными поверхностями, с помощью тройного интеграла: x = 0, z = x + y, y = 0, y = 1, y = 3.
4. Вычислить криволинейный интеграл по заданному контуру интегрирования: ∮ (xdx + ydy) L: y = x; A(0;0), B(1;1)
5. Является ли векторное поле F = { y + z; x + z; x + y } потенциальным? Если да, найти его скалярный потенциал.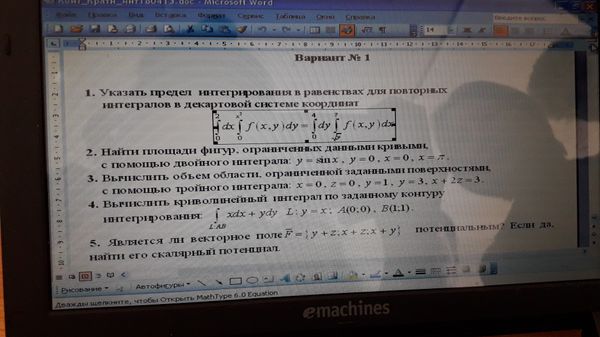
Решение
Это уравнение прямой х=2
см. рисунок.
2.
S= ∫ ∫ _(D)dxdy= ∫ ^(Pi)_(0)dx ∫^(sinx) _(0)dy=
= ∫ ^(Pi)_(0)( y)|^(sinx) _(0) dx=
= ∫ ^(Pi)_(0)(sinx-0)dx=-(cosx)| ^(Pi)_(0)=-(cos(Pi)-cos0)=2
3.
V= ∫ ∫ ∫ dxdydz= ∫^(3)_(1)dy ∫^(3)_(0)dx ∫^((3-x)/2) _(0)dz=
= ∫^(3)_(1)dy ∫^(3)_(0)(z)|^((3-x)/2) _(0)dx=
= ∫^(3)_(1)dy∫^(3)_(0)((3-x)/2 - 0)dx
= ∫^(3)_(1) ((3/2)x-(x^2/4))|^(3)_(0)dy=
=∫^(3)_(1)((9/2)-(9/4))dy=(9/4)(y)|^3_(1)=9/2=4,5