Задача 27956 ...
Условие
sin(5π/12) * cos(5π/12);
математика
1001
Решение
★
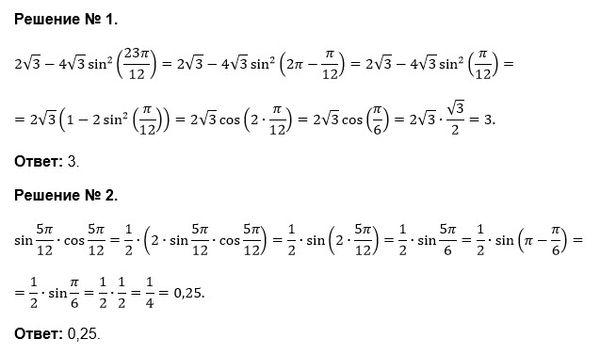
Все решения
sin^2 альфа=(1-сos2альфа)/2
sin^2(23Pi/12)=(1-cos(46Pi/12))/2=(1-сos(4Pi-(2Pi/12)))/2=
=(1-сos(Pi/6))/2=(1-sqrt(3)/2)/2=(2-sqrt(3))/4
О т в е т.
2sqrt(3)-4sqrt(3)*((2-sqrt(3))/4)=2sqrt(3)-2sqrt(3)+3=3
2
По формуле
sin2 альфа =2*sin альфа *cos альфа
⇒
sin альфа *cos альфа =(1/2)*sin2 альфа
О т в е т. (1/2)*sin(10Pi/12)=(1/2)*sin(5Pi/6)=(1/2)*(1/2)=1/4