Задача 14139 ...

u18825411027

03.03.2017

4
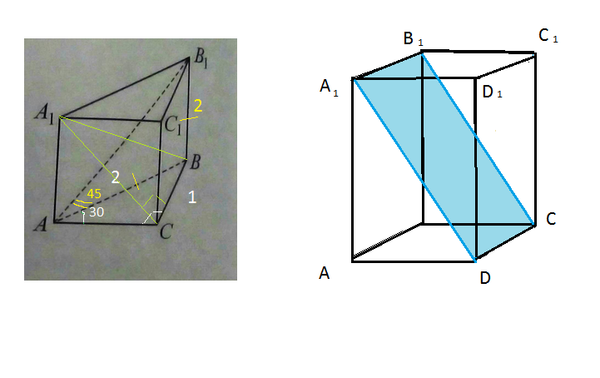
В основании прямой призмы
АВСА_1В_1С_1 - треугольник АВС, у ко-
торого ∠С = 90°, AB = 2, ∠ВАС = 30°.
В, AB = 45. Найдите площадь тре-
угольника АСВ.

1) 2√6
2) √5
3) 1-√
7
2
4) 3√4

5
Площадь основания правильной призмы
равна 1,5 см². Высота призмы равна 8 см. Найдите пла-
щадь сечения А_1В_1СD.

1) √3√3 см²
2) 12 см²
3) 0,5√3√3 см²
4) 14 см²

SOVA

04.03.2017

★

1.
Δ АВС:
ВС=(1/2)AB=1- катет против угла в 30 градусов равен половине гипотенузы.
АС=АВ*cos30 градусов=2*(sqrt(3)/2)=sqrt(3).

Δ АВB1:
AB=BB1=2 катеты равнобедренного прямоугольного треугольника ( острые углы по 45 градусов).

Δ АА1С:
А1С^2=(AA1)^2+AC^2=2^2+(sqrt(3)^2=7
A1C=sqrt(7)

AC⊥CB ⇒ A1C ⊥CB по теореме о трех перпендикулярах
Δ А1СB- прямоугольный
S ( Δ А1СB )= (1/2)A1C *CB=(1/2)*sqrt(7)*1=(1/2)sqrt(7)

О т в е т. 3) (1/2)sqrt(7)

2.
ABCD- квадрат
S(основания)=AD^2=DC^2=1,5 ⇒ CD=sqrt(1,5)=sqrt(3/2)
Δ АА1D:
A1D^2=A1A^2+AD^2=8^2+1,5=65,5=131/2
A1D=sqrt(131/2)
S(A1B1CD)=A1D*DC=sqrt(131/2)*(sqrt(3/2)=sqrt(393)/2

О т в е т. 3) 0,5 sqrt(393)